Find the correct angles to cut perfect geometric shapes including a pentagon, hexagon, heptagon, octagon, nonagon, decagon, and any other polygon.

Step One – Solve for X
The first step is to imagine there are a series of triangles that make up the polygon.
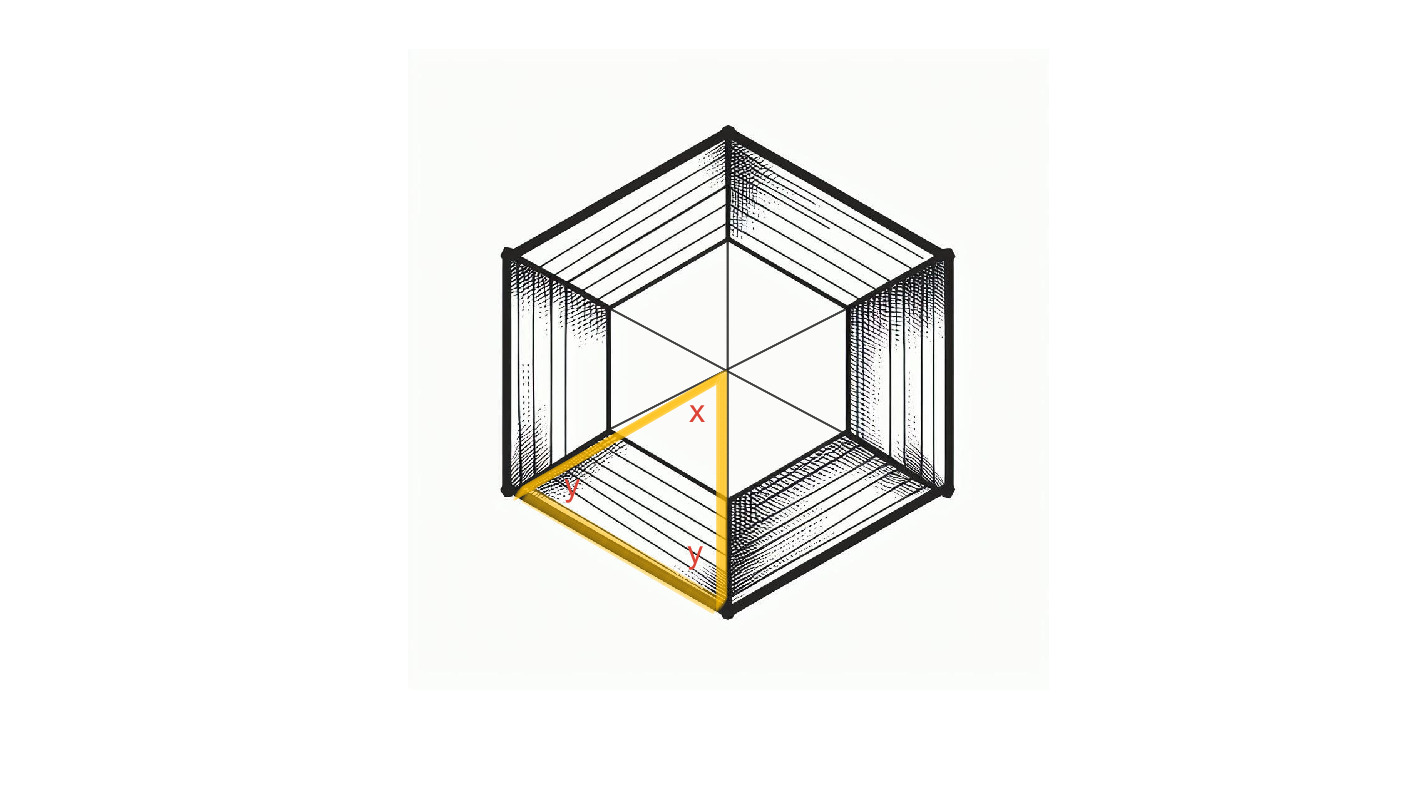
We know that the sum of the interior angles (in this case X) will always be 360. This means we can solve for X with this equation:
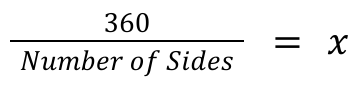
In this case we have 6 sides so we know: X = 60
Step Two – Solve for Y
Next we need to solve for y which will be the angle of our miter cuts. To find this angle we’ll need to use the next equation:
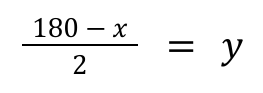
Since the interior angles of a triangle will always equal 180, we will need to subtract x from the first step and then divide by two because there are two equal y angles.
In our example hexagon, we would subtract 180 – 60 and then divide by two to get: y = 60
Surprise! They are equilateral triangles
All Kinds of Polygons
The calculation works the same for any polygon — as long as all the sides are the same length.
Now you can cut the sides to length and cut with your miter saw.